Rotate | Описание и примеры стандартных функций SVG

Для осуществления анимационных эффектов, связанных с вращением, увеличением фигур из центра, необходимо точно знать координаты центра вращения, а так же, в некоторых случаях, и длину периметра фигур. Рассмотрим правильные многоугольники: пятиугольник, шестиугольник, восьмиугольник и т.д. Ниже приведен пример шестиугольника, но все параметры, расчетные формулы одинаковы для любого правильного многоугольника, меняется только “n”

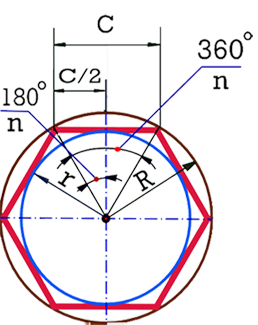
С – длина стороны многоугольника
n – число сторон
R – радиус описанной окружности
r – радиус вписанной окружности
Формулы расчета:
C = 2*R*sin(180°/n) = 2*r*tg(180°/n)
R = (c/2)/sin(180°/n) = r/cos(180°/n)
r = (c/2)*ctg(180°/n) = R*cos(180°/n)

Для вычисления центра вращения нужно, как-то определить заранее, хоть один параметр, например – длину стороны многоугольника – “C”.
Это можно сделать несколькими способами:

Вычисление длины одной из сторон правильного многоугольника

Для этого используем содержимое команды – path

1 2	<path d="M48.9 60.9 16.9 60.9 1.2 33.4 17.1 6.1 48.7 6.2 64.4 33.6z" style="fill:none;stroke-width:1;stroke:#dc143c"/>

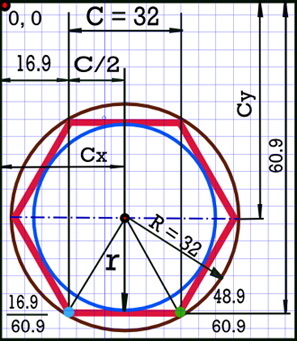Первая группа цифр после команды M (moveto) – M48.9 60.9 определяет координаты начальной (зеленой) точки стороны многоугольника. Вторая группа цифр – координаты конечной (синей) точки – 16.9 60.9 Вычисляем длину горизонтальной стороны многоугольника –
C = 48.9 – 16.9 = 32px
Вычисляем радиус описанной окружности шестиугольника:
R = (c/2)/sin(180°/n), где n=6
R = 16/sin(30°) = 32px
для шестиугольника – R = C

Вычисление центра вращения шестиугольника

Радиус вписанной окружности: r = R*cos(180°/n) = 32*cos(30°) = 27.71px

Для определения центра вращения шестиугольника необходимо расчитать параметры Cx, Cy.
Cx = 16.9 + С/2 = 32.9;
Cy = 60.9 – r = 60.9 – 27.71 = 33.19px;
Проверяем:

<path d="M48.9 60.9 16.9 60.9 1.2 33.4 17.1 6.1 48.7 6.2 64.4 33.6z"

style="fill:none;stroke-width:1;stroke:#dc143c"/>

</g>

Вычисление центра вращения пятиугольника

Открываем файл *.svg, созданный в векторном редакторе и находим строку кода, рисующую пятиугольник.

<path d="M38.8 31.3 69.4 53.6 57.6 89.5 19.7 89.5 8.1 53.6z"

style="fill:none; stroke:#f20404"/>

Начальная точка (зелёная) отрисовки пятиугольника имеет координаты – M38.8 31.3, далее по часовой стрелке, следующая вершина пятиугольника – 69.4 53.6

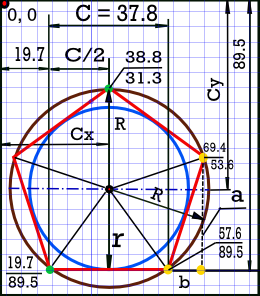Как и в примере с шестиугольником, легче всего вычислить длину горизонтальной стороны многоугольника (зелёная и жёлтая точки) – С = 57,6 – 19,7 = 37,9
Но это частный случай, когда сторона многоугольника паралелльна одной из осей ординат. В большинстве случаев сторона многоугольника идет под углом к осям ординат. Вычислим длину наклонной стороны, используя теорему Пифагора – с² = a² + b² На рисунке это треугольник с жёлтыми точками на вершинах. Так как начало координат (0,0) полотна SVG находится в левом верхнем углу, поэтому

a = 89.5 – 53.6 = 35.9 – из нижней точки вычитаются координаты “y” верхней точки

b = 69.4 – 57.6 = 11.8 – вычитаются координаты “x” двух вершин треугольника
c = √ 35.9² + 11.8² = 37.78

Определение радиусов вписанной и описанной окружностей по формулам из таблицы ниже

R = 0,851*C = 32.16px – радиус описанной вокруг пятиугольника окружности
r = 0688*C =26.0px – радиус вписанной в пятиугольник окружности

Определение координат центра вращения пятиугольника

Cx = 19.7 + C/2 = 19.7 +18.9 = 38.6px
Cy = 31.3 + R = 31.3 + 32.16 = 63.46px
Проверяем вычисленные центры вращения для пятиугольника и шестиугольника. Анимация начинается при наведении курсора мышки.
Первая и вторая картинка вращаются пока наведен курсор мышки. Третья картинка – увеличение. Четвертая – вращение и одновременное увеличение размеров изображения.

Таблица для вычисления параметров правильных многоугольников

n (число сторон)	c (сторона многоугольника)		R (радиус описанной окружности)		r (радиус вписанной окружности)		S (площадь многоугольника)
3	1,772*R	3,464*r	0,577*c	2,000*r	0,289*c	0,500*R	0,433*c²	1,299*R²	5,196*r²
4	1,414*R	2,000*r	0,707*c	1,414*r	0,500*c	0,707*R	1,000*c²	2,000*R²	4,000*r²
5	1,176*R	1,453*r	0,851*c	1,236*r	0,688*c	0,809*R	1,721*c²	2,378*R²	3,633*r²
6	1,000*R	1,155*r	1,000*c	1,155*r	0,866*c	0,866*R	2,598*c²	2,598*R²	3,464*r²
7	0,868*R	0,963*r	1,152*c	1,110*r	1,038*c	0,901*R	3,635*c²	2,736*R²	3,371*r²
8	0,765*R	0,828*r	1,307*c	1,082*r	1,207*c	0,924*R	4,828*c²	2,828*R²	3,314*r²
9	0,684*R	0,728*r	1,452*c	1,064*r	1,374*c	0,940*R	6,182*c²	2,893*R²	3,276*r²
10	0,618*R	0,650*r	1,618*c	1,052*r	1,539*c	0,951*R	7,694*c²	2,939*R²	3,249*r²
11	0,564*R	0,587*r	1,775*c	1,042*r	1,703*c	0,960*R	9,364*c²	2,974*R²	3,230*r²
12	0,518*R	0,536*r	1,932*c	1,035*r	1,866*c	0,966*R	11,196*c²	3,000*R²	3,215*r²
16	0,390*R	0,398*r	2,563*c	1,020*r	2,514*c	0,981*R	20,109*c²	3,062*R²	3,183*r²
20	0,313*R	0,317*r	3,196*c	1,013*r	3,157*c	0,988*R	31,569*c²	3,090*R²	3,168*r²
24	0,261*R	0,263*r	3,831*c	1,009*r	3,798*c	0,991*R	45,575*c²	3,106*R²	3,160*r²
32	0,196*R	0,197*r	5,101*c	1,005*r	5,077*c	0,995*R	81,225*c²	3,121*R²	3,152*r²
48	0,131*R	0,131*r	7,645*c	1,002*r	7,629*c	0,998*R	183,08*c²	3,133*R²	3,146*r²
64	0,098*R	0,098*r	10,190*c	1,001*r	10,178*c	0,999*R	325,69*c²	3,137*R²	3,144*r²

Расчетные данные взяты – здесь
⇚ Масштабирование векторных изображений
Позиционирование иконок SVG ⇛
Примеры анимация многоугольников ⇛

Хочу начать с самого простого и надежного вида анимации, которая корректно отображается почти во всех браузерах, даже в IE6 🙂
это – “animateTransform attributeName=”transform” type=”rotate” – поворот объекта на заданный угол вокруг точки.

Первое число в параметре from=”0 100 100″ to=”360 100 100″ в команде “rotate” это градусы, на который будет повернут объект. Положительное значение повернёт объект по часовой стрелке, отрицательное – против часовой стрелки. Вторые и третьи числа это координаты точки, относительно которой будет произведен поворот.

Продолжить чтение →

Описание и примеры стандартных функций SVG

Маски, градиенты, фильтры, анимация, вертикальный и горизонтальный parallax

Архивы с меткой: rotate

Анимация многоугольников

Определение центра вращения фигур

Анимация иконки – разбитое сердце

Анимация линии SVG